Dynamische Makroökonomik, stochastisches Wachstumsmodell [Datum: 01-06-10]

Dieses Batch-File löst das stochastische Wachstumsmodell mit endogenem Arbeitsangebot und stellt Wertfunktionen aus den Iterationsschritten sowie die Politikfunktion graphisch dar;

Contents

Sauberer Arbeitsplatz

clc
clear
close all

Modell:

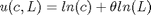
$u(c,L) = ln(c) + \theta ln(L)$

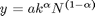
$y =a k^\alpha N^{(1-\alpha)}$

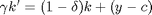
$\gamma k' = (1-\delta) k + (y-c)$

Definiere Modellparameter

beta = (984/1000); % Diskontfaktor
alpha = 1/3; % Anteil des Faktors Kapital am Volkseinkommen
delta = 1/40; % Abschreibungsrate
theta = 3.48;% Arbeitsleid: so gewählt, dass der steady state Arbeitseinsatz
            % 0.2*24[Stunden/Tag]*7[Tage/Woche]*52/45[Woche/Arbeitswoche]=39 Stunden pro Arbeitswoche beträgt
gamma = 1.004; % Arbeitsvermehrendes Trendwachstum
rho = 0.979; % Autokorrelation
sigma_e = 0.0072; % Standardabweichung der Produktivitätsschocks

Definiere Programmparameter

Nk=500;
Na=17;
addpath('..\Tauchen\')

Erstellen des Produktivitätsgitters

[a_grid,P]=Tauchen(rho,Na,1,0, 'equi');
a_grid=exp(a_grid*(sigma_e/sqrt(1-rho^2)));

Berechne steady state Kapitaleinsatz

Bedingungen erster Ordnung: Intertemporale Optimalität 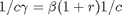$1/c \gamma = \beta (1+r) 1/c$

somit: 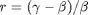$r=(\gamma-\beta)/\beta$

Optimaler Kapitaleinsatz 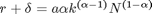$r + \delta = a \alpha k^{(\alpha-1)} N^{(1-\alpha)}$

Also: 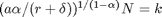$(a \alpha / (r + \delta))^{1/(1- \alpha)}N = k$

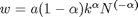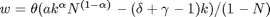
Optimaler Arbeitseinsatz: $w = a (1-\alpha) k^{\alpha} N^{(-\alpha)}$, $w = \theta (a k^\alpha N^{(1-\alpha)} -(\delta+\gamma-1) k) / (1-N)$

Einsetzen:

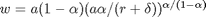$w = a (1-\alpha) (a \alpha / (r + \delta))^{\alpha/(1- \alpha)}$,

$N=(( (1-\alpha))/(1-\alpha+\theta[1-(\delta+\gamma-1)(( \alpha/(r+\delta)))]))$

r = (gamma-beta)/beta; % Zinssatz
Nss = (1-alpha)/(1-alpha+theta*(1-(delta+gamma-1)*(alpha/(r+delta)))); %Steady state Arbeitseinsatz
Kss = (alpha / (r + delta))^(1/(1- alpha))*Nss; % Steady State Kapitaleinsatz
Yss = Kss^alpha* Nss^(1-alpha); % Steady state output

Lege ein Gitter für K fest

Kmax=a_grid(end)^(1/(1- alpha))*Kss; % Maximaler Kapitalstock steady state +300%
Kmin=a_grid(1)^(1/(1- alpha))*Kss; % Minimaler Kapitalstock steady stae -80%
aux=norminv(1/20:18/20/(Nk-1):19/20);
k_grid=Kss*exp(2*aux./aux(end)*log(Kmax/Kss)); % Gitter mit vielen Punkten in der Mitte

Finde zunächst den optimalen Arbeitseinsatz gegeben k und k'

Bedingungen erster Ordnung für optimalen Arbeitseinsatz:

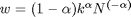$w = (1-\alpha) k^{\alpha} N^{(-\alpha)}$ (Arbeitsnachfrage)

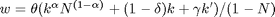$w = \theta (k^\alpha N^{(1-\alpha)} +(1-\delta) k + \gamma k') / (1-N)$ (Arbeitsangebot)

empl=NaN(Na,Nk,Nk);
sigma=NaN(Na,Nk,Nk); %Nutzen bei optimalem Arbeitseinsatz

Variante 1: Maximieren ohne Gitter

% for m=1:Na
%     for i=1:Nk
%         max_y=a_grid(m)*k_grid(i).^alpha+(1-delta).*k_grid(i); %Resourcen bei $N = 1$
%         for j=1:Nk
%             if max_y>k_grid(j)*gamma % Nur Investitionspläne betrachten die bei vollem Arbeitseinsatz durchführbar sind
%                 [empl(m,j,i) sigma(m,j,i)] = fminbnd(@(n)(util(n,k_grid(i),...
%                     k_grid(j),theta,alpha,gamma,delta,a_grid(m))),0.00000001,.99999999999);
%             else
%                 empl(m,j,i)  = 1;
%                 sigma(m,j,i) = Inf;
%             end
%         end
%     end
% end
% sigma=-sigma; % -Zielfunktion wurde minimiert

Code der Unterfunktion util

% function u=util(n,k,kprime,theta,alpha,gamma,delta,a)
%
% c=a* k.^alpha .* n.^(1-alpha) + (1-delta) .* k - gamma .* kprime;
%
% u=log(c)+theta*log(1-n);
%
% u(c<0)=-Inf;
%
% u=-u;

Variante 2: Optimale Beschäftigung auf einem Gitter finden

NN=1000;
n_grid=linspace(0,1,NN);
aux1=gamma.*repmat(k_grid',1,NN);
aux2=theta*repmat(log(1-n_grid),Nk,1);
aux3=repmat(n_grid.^(1-alpha),Nk,1);
for m=1:Na
    for i=1:Nk

        c=a_grid(m).* k_grid(i).^alpha *aux3  + (1-delta) .* k_grid(i) - aux1;
        u=log(c)+aux2;
        u(c<0)=-Inf;
        [sigma(m,:,i) empl(m,:,i)]=max(u,[],2);

    end
end
empl=n_grid(empl);

Wertfunktionsiteration

dist=99;
V=zeros(Na,Nk); %Initialisiere die Werfunktion
t=1;
while dist>0.001
    EV=P*V;
    [Vnew pol]=max(sigma+beta*repmat(EV,[1,1,Nk]),[],2);
    Vnew=squeeze(Vnew);
    pol=squeeze(pol);
    dist=max(max(abs(Vnew-V)));
    V=Vnew;
end

Graphische Darstellung

figure(1)
surf(k_grid,a_grid,V)
title('Wertfunktion')
xlabel('Kapitalstock')
ylabel('Produktivität')



figure(2)
scrsz = get(0,'ScreenSize');
set(2,'Position',scrsz)
title('Politikfunktion')
xlabel('Kapitalstock in t')
ylabel('Kapitalstock in t+1')
plot((k_grid),(k_grid(pol([1 ceil(Na/2) end],:))))
hold on
plot(([Kmin Kmin]),([k_grid(1)*.9 k_grid(end)*1.1]),'b--')
plot(([Kss Kss]),([k_grid(1)*.9 k_grid(end)*1.1]),'g--')
plot(([Kmax Kmax]),([k_grid(1)*.9 k_grid(end)*1.1]),'r--')
plot(([k_grid(1)*.95 k_grid(end)*1.05]),([k_grid(1)*.95 k_grid(end)*1.05]),'k')
legend({' k_{t+1}(k_t,A_t) falls \newline A_t minimal', ' k_{t+1}(k_t,A_t) falls \newline A_t durchs.',...
    ' k_{t+1}(k_t,A_t) falls \newline A_t maximal', ' steady state k falls \newline A immer minimal',...
    ' steady state k falls \newline A immer durchs.', ...
    ' steady state k falls \newline A immer maximal', '45° Linie'},'Location','EastOutside')

Simulation

Ziehe 5000+500 Shocks auf die Produktivität, berechne jeweils den aus der Politikfunktion folgenden Kapitalstock, bestimme zu letzt Investitionen, Konsum, Löhne, etc.

T=5000; % Simulationsperiode
tau=500; % Initialisationsperiode
schock=rand(1,T+tau); % Schocks (0,1)-gleichverteilt
PR=cumsum(P,2); % Kummulierte Übergangswahrscheinlichkeiten
kapital_index=ones(1,T+tau)*ceil(Nk/2); %initialisiere Kapitalvariable auf ca. ss Niveau
a_ind=ones(1,T+tau)*ceil(Na/2);
n=zeros(1,tau+T);

% Die Timing Annahme hier ist, dass _Kapital_index_ den zukünftigen
% Kapitalstock mißt.

for t=2:T+tau
    a_ind(t)=min(max(1,sum(PR(a_ind(t-1),:)<schock(t))+1),Na);
    kapital_index(t)=pol(a_ind(t),kapital_index(t-1)); % Neuer Kapitalstock
    n(t)=empl(a_ind(t),kapital_index(t),kapital_index(t-1));
end

kapital=k_grid(kapital_index(tau:end-1)); %In periode t=1...T zur Produktion eingesetzt
a=a_grid(a_ind(tau+1:end)); % Produktivität in t=1...T
n(1:tau)=[]; % Lösche die ersten tau Einträge (Beschäftigung für t=1...T)
y=a.*kapital.^(alpha).*n.^(1-alpha); % Output
I=k_grid(kapital_index(tau+1:end))-(1-delta).*kapital; % Investitionen

c=y-I; % Konsum
w = (1-alpha)*y./n;
r = alpha*y./kapital - delta;

figure(3)
plot(1:100,[log(y(1:100)); log(c(1:100)); log(I(1:100))]);
title('Simulierte Zeitreihe für Aggregate')
legend({'Output', 'Konsum', 'Investitionen'})

Auswertung

logDaten=[log(y); log(c); log(I); log(n); log(w); r];
trend=myhpfilter(logDaten',1600);

Konjunktur=(logDaten'-trend);


[T nvar]=size(Konjunktur);
Zweitmomente(:,1)=std(Konjunktur)';
Zweitmomente(:,2)=std(Konjunktur)'./std(Konjunktur(:,1));
Zweitmomente(:,3)=corr(Konjunktur,Konjunktur(:,1))';
for j=1:nvar
Zweitmomente(j,4)=corr(Konjunktur(2:end,j),Konjunktur(1:end-1,j));
end
Zweitmomente

Zweitmomente =

    0.0179    1.0000    1.0000    0.7187
    0.0074    0.4106    0.8933    0.7856
    0.0712    3.9773    0.9742    0.6911
    0.0095    0.5286    0.9590    0.6754
    0.0092    0.5153    0.9568    0.7666
    0.0008    0.0458    0.9471    0.6993


Published with MATLAB® 7.9