Dynamische Makroökonomik, stochastisches Wachstumsmodell mit hoher Substitutionselastizität

Dieses Batch-File löst das stochastische Wachstumsmodell mit endogenem Arbeitsangebot und endogener Nutzungsintensität des Kapitals und stellt Wertfunktionen sowie die Politikfunktion graphisch dar. Anscließend wird die so numerisch modellierte Ökonomie simuliert, ein Zeitpfad für Investitionen, Konsum und Output dargestellt und die üblichen RBC konjunkturstatistiken berechnet.

Autor: Christian Bayer, Datum: 06-06-2010

Contents

Sauberer Arbeitsplatz

clc
clear
close all

Modell:

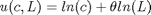
$u(c,L) = ln(c) + \theta ln(L)$

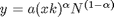
$y =a (xk)^\alpha N^{(1-\alpha)}$

$\gamma k' = (1-\delta(x)) k + (y-c)$

$\delta=\delta_0 + \delta_1/(1-\xi) x^{(1-\xi)} $

Definiere Modellparameter

beta = (984/1000); % Diskontfaktor
alpha = 1/3; % Anteil des Faktors Kapital am Volkseinkommen
delta = 1/40; % Abschreibungsrate
theta = 4.2;% Arbeitsleid: so gewählt, dass der steady state Arbeitseinsatz
            % 0.2*24[Stunden/Tag]*7[Tage/Woche]*52/45[Woche/Arbeitswoche]=39 Stunden pro Arbeitswoche beträgt
gamma = 1.004; % Arbeitsvermehrendes Trendwachstum
rho = 0.979; % Autokorrelation
sigma_e = 0.002; % Standardabweichung der Produktivitätsschocks
ksi=0.1; %"Elsatizität" der Abschreibungsrate

Definiere Programmparameter

Nk=1000;
Na=23;
addpath('..\Tauchen\')

Abschreibungsfunktionsparameter

Langfristige Optimalität

$ r+\delta(x)+\delta_0*(1+\xi) = \delta(x)*(1+\xi)$

$ \delta_0 =[0.025 *\xi - r]/(1+\xi)$

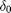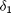Wähle $\delta_0$ und $\delta_1$ so, dass die steady state Intensität 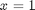$x=1$ und die Abschreibungsrate 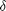$\delta$ sind.

r = (gamma-beta)/beta; % Zinssatz
delta_0 = (delta*ksi-r)/(1+ksi);
delta_1 =(1+ksi)*(delta-delta_0);

Bestimme die Parameter der semi-reduzierten Produktionsfunktion

alpha_star=alpha*ksi/(1+ksi-alpha);

Erstellen des Produktivitätsgitters

[a_grid,P]=Tauchen(rho,Na,1,0, 'equi');
a_grid=exp(a_grid*(sigma_e/sqrt(1-rho^2)));
a_grid_star=exp((1+ksi)/(1+ksi-alpha)*log(a_grid))*(alpha/delta_1).^(alpha/(1+ksi-alpha));

Berechne steady state Kapitaleinsatz

Bedingungen erster Ordnung: Intertemporale Optimalität 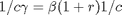$1/c \gamma = \beta (1+r) 1/c$

somit: 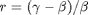$r=(\gamma-\beta)/\beta$

Optimaler Kapitaleinsatz 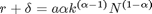$r + \delta = a \alpha k^{(\alpha-1)} N^{(1-\alpha)}$

Also: 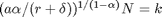$(a \alpha / (r + \delta))^{1/(1- \alpha)}N = k$

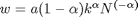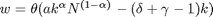
Optimaler Arbeitseinsatz: $w = a (1-\alpha) k^{\alpha} N^{(-\alpha)}$, $w = \theta (a k^\alpha N^{(1-\alpha)} -(\delta+\gamma-1) k)$

Einsetzen:

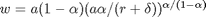$w = a (1-\alpha) (a \alpha / (r + \delta))^{\alpha/(1- \alpha)}$,

$N=(( (1-\alpha))/(\theta[1-(\delta+\gamma-1)(( \alpha/(r+\delta)))]))$

Nss = (1-alpha)/(theta*(1-(delta+gamma-1)*(alpha/(r+delta)))); %Steady state Arbeitseinsatz
Kss = (alpha / (r + delta))^(1/(1- alpha))*Nss; % Steady State Kapitaleinsatz

Yss = Kss^alpha* Nss^(1-alpha); % Steady state output

Lege ein Gitter für K fest

Kmax=a_grid(end)^(1/(1- alpha))*Kss; % Maximaler Kapitalstock steady state +300%
Kmin=a_grid(1)^(1/(1- alpha))*Kss; % Minimaler Kapitalstock steady stae -80%
aux=norminv(1/20:18/20/(Nk-1):19/20);
k_grid=Kss*exp(8*aux./aux(end)*log(Kmax/Kss)); % Gitter mit vielen Punkten in der Mitte

Finde zunächst den optimalen Arbeitseinsatz gegeben k und k'

Bedingungen erster Ordnung für optimalen Arbeitseinsatz:

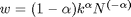$w = (1-\alpha) k^{\alpha} N^{(-\alpha)}$ (Arbeitsnachfrage)

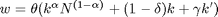$w = \theta (k^\alpha N^{(1-\alpha)} +(1-\delta) k + \gamma k')$ (Arbeitsangebot)

Optimale Beschäftigung auf einem Gitter finden

empl=NaN(Na,Nk,Nk);
sigma=NaN(Na,Nk,Nk); %Nutzen bei optimalem Arbeitseinsatz
NN=2000;
n_grid=linspace(0,1,NN);
aux1=gamma.*repmat(k_grid',1,NN);
aux2=-theta*repmat(n_grid,Nk,1);
aux3=repmat(n_grid.^(1-alpha_star),Nk,1);
for m=1:Na
    for i=1:Nk
        y=a_grid_star(m).*k_grid(i).^alpha_star .*aux3;
        delta_x=alpha*y./k_grid(i)./(1+ksi)+delta_0;
        c=y + (1-delta_x).*k_grid(i) - aux1;
        u=log(c)+aux2;
        u(c<0)=-Inf;
        [sigma(m,:,i) empl(m,:,i)]=max(u,[],2);

    end
end
empl=n_grid(empl);

clear aux* y c u

Wertfunktionsiteration

dist=99;
V=zeros(Na,Nk); %Initialisiere die Werfunktion
t=1;
while dist>0.001
    EV=P*V;
    [Vnew pol]=max(sigma+beta*repmat(EV,[1,1,Nk]),[],2);
    Vnew=squeeze(Vnew);
    pol=squeeze(pol);
    dist=max(max(abs(Vnew-V)));
    V=Vnew;
end

Graphische Darstellung von Wert- und Politikfunktion

figure(1)
surf(k_grid,a_grid,V)
title('Wertfunktion')
xlabel('Kapitalstock')
ylabel('Produktivität')


figure(2)
scrsz = get(0,'ScreenSize');
set(2,'Position',scrsz)
title('Politikfunktion (log-Skala)')
xlabel('Kapitalstock in t')
ylabel('Kapitalstock in t+1')
plot(log(k_grid),log(k_grid(pol([1 ceil(Na/2) end],:))))
hold on
plot(log([Kmin Kmin]),log([k_grid(1)*.9 k_grid(end)*1.1]),'b--')
plot(log([Kss Kss]),log([k_grid(1)*.9 k_grid(end)*1.1]),'g--')
plot(log([Kmax Kmax]),log([k_grid(1)*.9 k_grid(end)*1.1]),'r--')
plot(log([k_grid(1)*.95 k_grid(end)*1.05]),log([k_grid(1)*.95 k_grid(end)*1.05]),'k')
legend({' k_{t+1}(k_t,A_t) falls \newline A_t minimal', ' k_{t+1}(k_t,A_t) falls \newline A_t durchs.',...
    ' k_{t+1}(k_t,A_t) falls \newline A_t maximal', ' steady state k falls \newline A immer minimal',...
    ' steady state k falls \newline A immer durchs.', ...
    ' steady state k falls \newline A immer maximal', '45° Linie'},'Location','EastOutside')

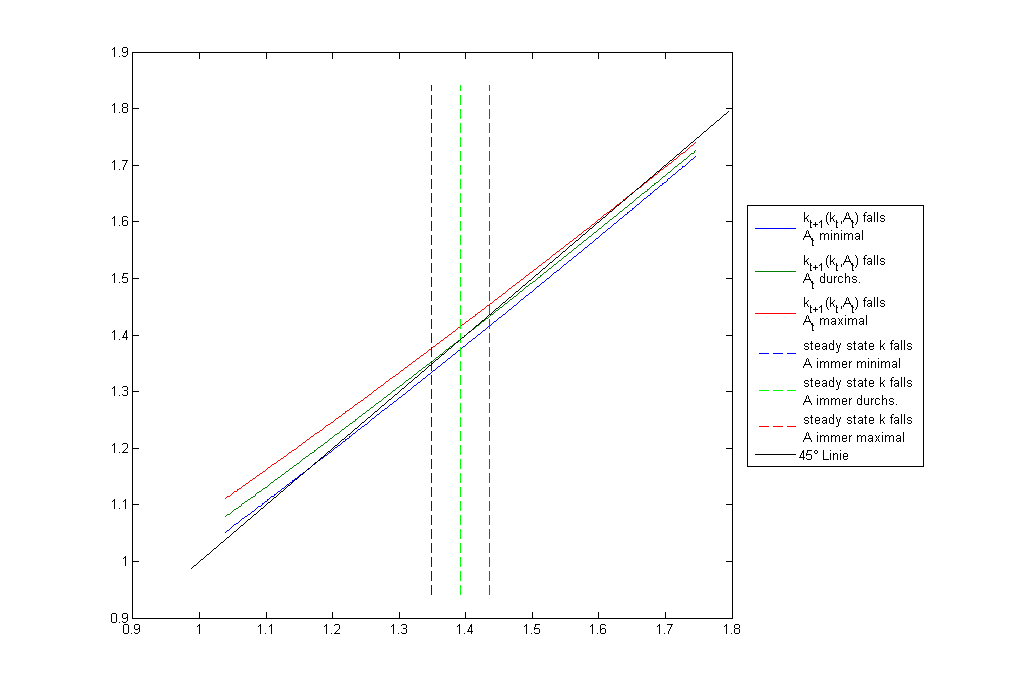
Simulation

Ziehe 5000+500 Shocks auf die Produktivität, berechne jeweils den aus der Politikfunktion folgenden Kapitalstock, bestimme zu letzt Investitionen, Konsum, Löhne, etc.

T=5000; % Simulationsperiode
tau=500; % Initialisationsperiode
schock=rand(1,T+tau); % Schocks (0,1)-gleichverteilt
PR=cumsum(P,2); % Kummulierte Übergangswahrscheinlichkeiten
kapital_index=ones(1,T+tau)*ceil(Nk/2); %initialisiere Kapitalvariable auf ca. ss Niveau
a_ind=ones(1,T+tau)*ceil(Na/2);
n=zeros(1,tau+T);

% Die Timing Annahme hier ist, dass _Kapital_index_ den zukünftigen
% Kapitalstock mißt.

for t=2:T+tau
    a_ind(t)=min(max(1,sum(PR(a_ind(t-1),:)<schock(t))+1),Na);
    kapital_index(t)=pol(a_ind(t),kapital_index(t-1)); % Neuer Kapitalstock
    n(t)=empl(a_ind(t),kapital_index(t),kapital_index(t-1));
end

kapital=k_grid(kapital_index(tau:end-1)); %In periode t=1...T zur Produktion eingesetzt
a=a_grid(a_ind(tau+1:end)); % Produktivität in t=1...T
n(1:tau)=[]; % Lösche die ersten tau Einträge (Beschäftigung für t=1...T)
y=a.*kapital.^(alpha).*n.^(1-alpha); % Output
I=k_grid(kapital_index(tau+1:end))-(1-delta).*kapital; % Investitionen

c=y-I; % Konsum
w = (1-alpha)*y./n;
r = alpha*y./kapital - delta;

Graphische Darstellung eines Zeitpfades für Output, Konsum, Investitionen

figure(3)
plot(1:100,[log(y(1:100)); log(c(1:100)); log(I(1:100))]);
title('Simulierte Zeitreihe für Aggregate')
legend({'log Output', 'log Konsum', 'log Investitionen'})

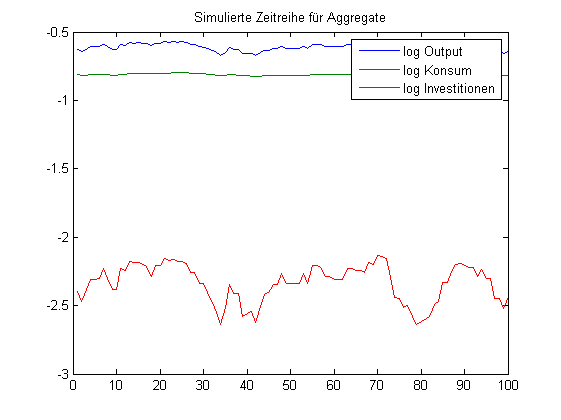
Auswertung im Sinne von Konjunkturstatistiken

logDaten=[log(y); log(c); log(I); log(n); log(w); r];
trend=myhpfilter(logDaten',1600);

Konjunktur=(logDaten'-trend);


[T nvar]=size(Konjunktur);
Zweitmomente(:,1)=std(Konjunktur)';
Zweitmomente(:,2)=std(Konjunktur)'./std(Konjunktur(:,1));
Zweitmomente(:,3)=corr(Konjunktur,Konjunktur(:,1))';
for j=1:nvar
Zweitmomente(j,4)=corr(Konjunktur(2:end,j),Konjunktur(1:end-1,j));
end
Zweitmomente

Zweitmomente =

    0.0171    1.0000    1.0000    0.6902
    0.0035    0.2038    0.9265    0.7293
    0.0803    4.6920    0.9916    0.6843
    0.0217    1.2675    0.9843    0.6831
    0.0057    0.3336   -0.7422    0.7617
    0.0008    0.0486    0.9325    0.6973


Published with MATLAB® 7.9